Skip to main content

StaticTyping

rascal-0.34.0

Synopsis​

The static type system of Rascal.

Description​

Rascal is based on static typing, this means that as many errors and inconsistencies as possible are spotted before the program is executed.

The Type Lattice​

The types are ordered in a so-called type lattice shown in the following figure.

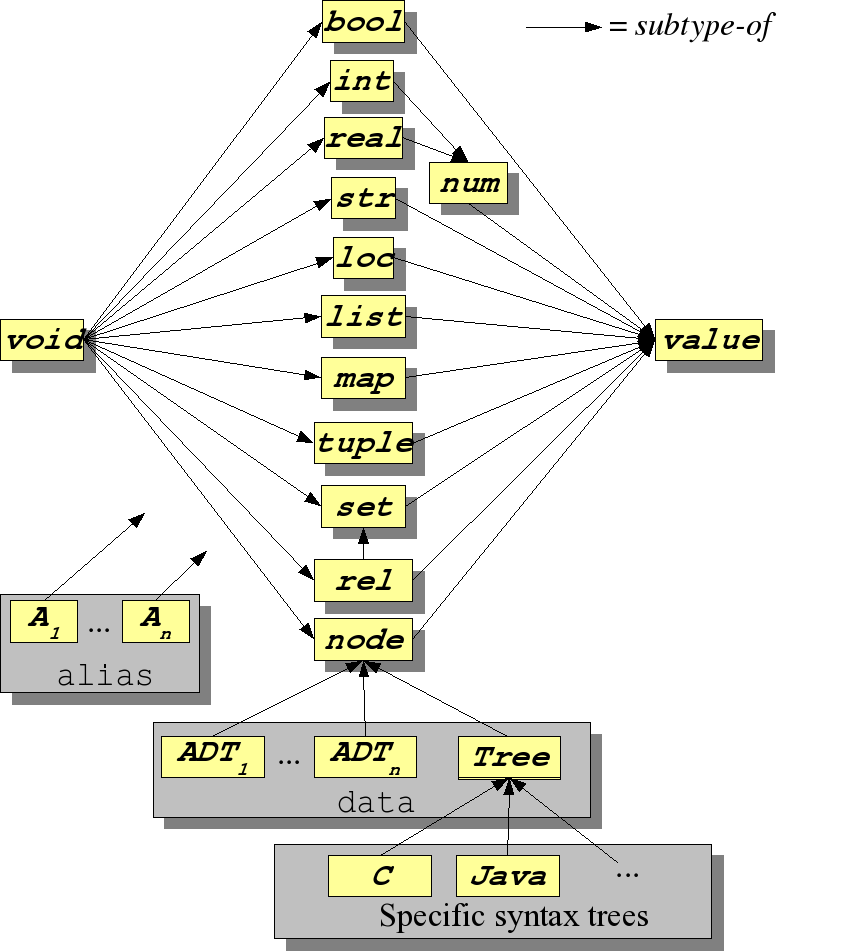
type-lattice.png

The arrows describe a subtype-of relation between types. The type void is the smallest type and is included in all other types and the type value is the largest type that includes all other types. We also see that rel is a subtype of set and that each ADT is a subtype of node. A special role is played by the datatype Tree that is the generic type of syntax trees. Syntax trees for specific languages are all subtypes of Tree. As a result, syntax trees can be addressed at two levels:

  • in a generic fashion as Tree and,
  • in a specific fashion as a more precisely typed syntax tree. Finally, each alias is structurally equivalent to one or more specific other types.

The fact that the types are ordered in a lattice makes it possible to define a Least Upper Bound (lub) on types. Given two types T₁ and T₂, lub(T₁, T₂) is defined as the nearest common super type of T₁ and T₂ in the type lattice.

Advanced Features​

The Rascal type system has various advanced features that are described separately:

  • Types may be be parameterized resulting in very general and reusable types, see Type Parameters.
  • Declarations of Functions and Algebraic Data Types may be parameterized and Type Constraints can be used to define constraints on the actual type to be used.
  • The formal arguments of functions are bound to values but in exceptional cases a function may need a type as argument value, ReifiedTypes make this possible.

Examples​

Here are some simple examples of correct and incorrect typing:

We can assign an integer value to an integer variable:

rascal>int i = 3;
int: 3

But assigning a string value gives an error:

rascal>int j = "abc";
|prompt:///|(4,9,<1,4>,<1,13>): Expected int, but got str
Advice: |https://www.rascal-mpl.org/docs/Rascal/Errors/CompileTimeErrors/UnexpectedType|
ok

The num type accepts integer and real values:

rascal>num n = i;
num: 3
rascal>n = 3.14;
num: 3.14

A variable of type value accepts all possible values:

rascal>value v = true;
value: true
rascal>v = "abc";
value: "abc"
rascal>v = [1, 2, 3];
value: [1,2,3]