Relation
Synopsis
An unordered set of tuples.
Description
In mathematics, given sets D₁, D₂, ... Dₙ, a n-ary relation R is characterized by R ⊆ D₁ × D₂ × ... × Dₙ. In other words, R consists of a set of tuples < V₁, ..., Vₙ > where each Vᵢ is an element of the set Dᵢ. When n = 2, we call the relation a binary relation
In database theory, a relation is a table with a heading and an unordered set of tuples:
| D₁ Name₁ | D₂ Name₂ | ... | Dₙ Nameₙ |
|---|---|---|---|
| V₁₁ | V₁₂ | ... | V₁ₙ |
| V₂₁ | V₂₂ | ... | V₂ₙ |
| V₃₁ | V₃₂ | ... | V₃ₙ |
| ... | ... | ... |
In Rascal, a relation is a set of tuples and is characterized by the type:
rel[D₁ Name₁, D₂ Name₂, ..., Dₙ Nameₙ]
See Relation Values and for a description of relations and their operators
(since relations are sets all set operators also apply to them, see Set Values)
and functions on relations
(and here again, since relations are sets all set operators also apply to them,
see functions on sets).
Relations in Daily Life
- The parent-of or friend-of relation between people.
 credit
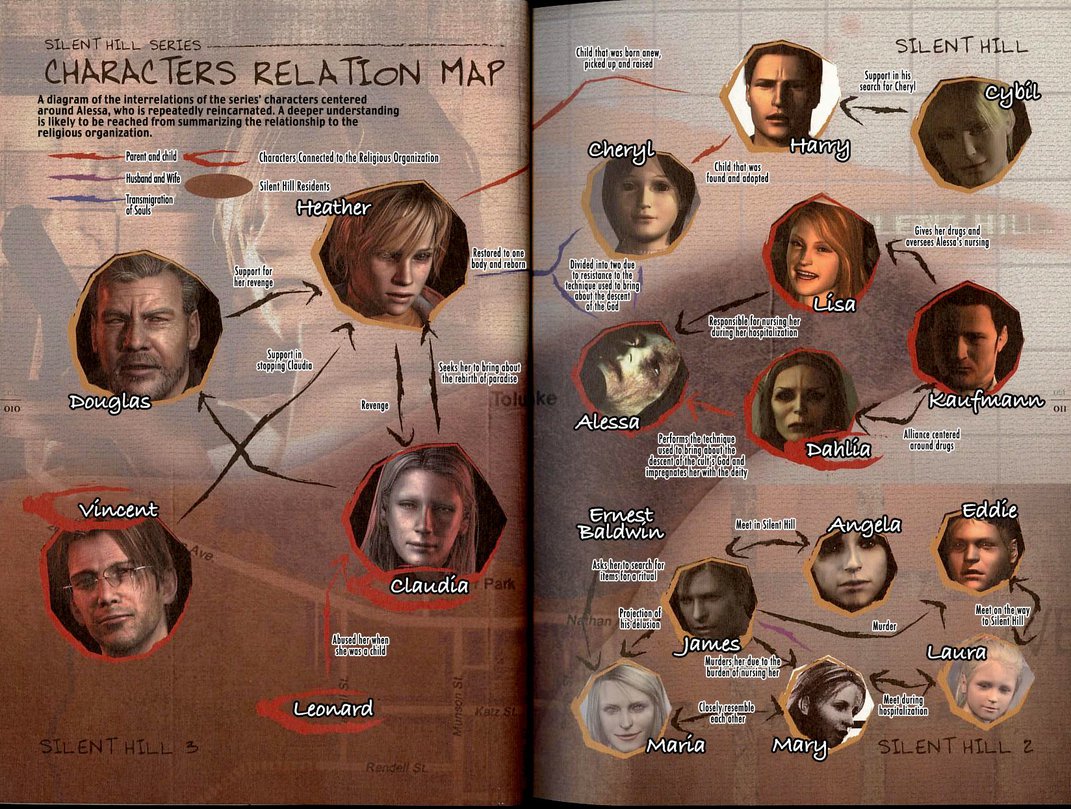
credit - A character relation map, describing the relations between the characters in a play or soap series.
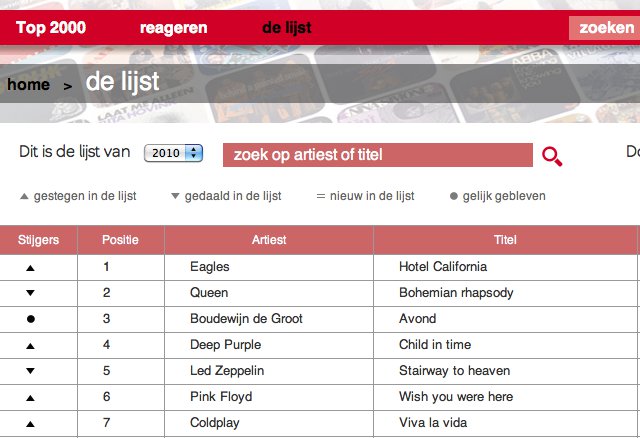
- A listing of the top 2000 songs of all times including the position, artist name, song title, the year the song was published.
 credit
credit
Relations in computer science
- A relational data base.
- Login information including user name, password, home directory, etc.
Relations in Rascal
- A parent child relation:
rel[str parent, str child] = {
<"Paul", "Eva">,
<"Paul", "Thomas">,
<"Jurgen", "Simon">,
<"Jurgen", "David">,
<"Tijs", "Mats">
};
- A fragment of the top 2000 relation:
rel[int position, str artist, str title, int year] Top2000 = {
<1, "Eagles", "Hotel California",1977>,
<2, "Queen", "Bohemian rhapsody", 1975>,
<3, "Boudewijn de Groot", "Avond", 1997>,
...
};